Answer:
Therefore the speed of automobile when it was driving from A to B was 50 km/ h.
Step-by-step explanation:
Given that,
An automobile covered the distance of 240 km between A and B with a certain speed.
Let the speed of the automobile be x km/hour.
We know that,
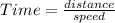
Time taken to travel from A to B point is
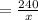 hours.
hours.
On its back, the automobile covered half of distance= 120 km at the same speed and for the trip he increased his speed 10 km/hour.
Time taken to complete the trip is
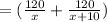 hours
hours
The driver took
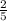 of an hour less when he come back.
of an hour less when he come back.
According to problem,
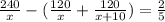
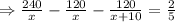
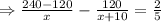
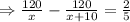
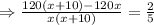
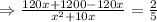
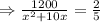
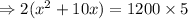
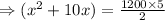
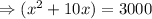
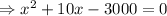
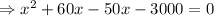
⇒x(x+60)-50(x+60)=0
⇒(x+60)(x-50)=0
⇒x= -60, 50
The speed could not negative.
So, x=50
Therefore the speed of automobile when it was driving from A to B was 50 km/ h.