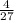Question

In a certain Algebra 2 class of 27 students, 11 of them play basketball and 9 of them play baseball. There are 11 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?

Answer 1

The probability of students who play both basketball and baseball =
`(4)/(27)`

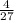
Explanation:

In a certain Algebra class,

The total number of students = 27 students

Let the students playing basketball be represented as A and baseball as B.

The students who play basketball, A= 11

The students who play basetball,B =9

The students who play neither sport, = 11

The students who play both basketball and baseball, = ?

By formula, P(AUB)=P(A)+P(B)-P(A∩B)

Substituting the values in the equation, we get

P(AUB) =
`(11)/(27) + (9)/(27) - (16)/(27)`

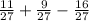
P(AUB) =
`(4)/(27)`

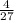
The probability of students who play both basketball and baseball =
`(4)/(27)`