Question

ABCD is a trapezoid. Solve for x and y ​

Answer 1

Given:

The given figure ABCD is a trapezoid.

The measure of ∠A is (2x + 32).

The measure of ∠B is 112°

The measure of ∠C is y.

The measure of ∠D is 46°

We need to determine the value of x and y.

Value of x:

We know the property that the adjacent angles in a trapezoid are supplementary.

Thus, we have;

`\angle A+\angle B=180`

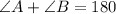
Substituting the values, we get;

`2x+32+112=180`

`2x+144=180`

`2x=36`

`x=18`

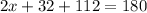
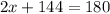
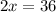
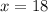
Thus, the value of x is 18.

Value of y:

The value of y can be determined using the property that the adjacent angles of a trapezoid are supplementary.

Thus, we have;

`\angle C+\angle D=180`

`y+46=180`

`y=134`

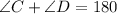
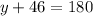
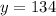
Thus, the value of y is 134.

Hence, Option c is the correct answer.