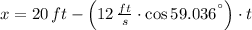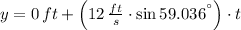Question

Margot is walking in a straight line from a point 20 feet due east of a statue in a park toward a point 12 feet due north of the statue. She walks at a constant speed of 5 feet per second. (a) Write parametric equations for Margot's position t seconds after she starts walking.

Answer 1

a)
`x = 20\,ft - \left(12\,\frac{ft}s}\cdot \cos 59.036^(\textdegree) \right)\cdot t`,
`y = 0\,ft +\left(12\,(ft)/(s)\cdot \sin 59.036^(\textdegree)\right)\cdot t`

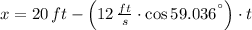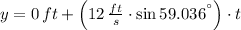
Explanation:

Let consider +x and +y the north and east directions. Given that Margot travels at constant speed, the formula is:

`v = (s)/(t)`

Where:

`t` - Time, in seconds.

`s` - Travelled distance, in meters.

The traveled distance is:

`s = v\cdot t`

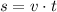
a) The parametric equations are described below:

`x = 20\,ft - \left(12\,\frac{ft}s}\cdot \cos 59.036^(\textdegree) \right)\cdot t`

`y = 0\,ft +\left(12\,(ft)/(s)\cdot \sin 59.036^(\textdegree)\right)\cdot t`