Question

An airplane pilot fell 390 m after jumping from an aircraft without his parachute opening. He landed in a snowbank, creating a crater 1.2 m deep, but survived with only minor injuries. Assume that the pilot's mass was 82 kg and his speed at impact was 50 m/s . Model him as a particle.a) Estimate the work done by the snow in bringing him to rest. b) Estimate the average force exerted on him by the snow to stop him. c) Estimate the work done on him by air resistance as he fell.

Answer 1

a) 101536 J

b) 84613 N

c) 210904 J

Step-by-step explanation:

a)Right before the impact, the pilot has a kinetic energy of:

`E_k = mv^2/2 = 82*50^2/2 = 102500 J`

The snow did some work to slow his speed/kinetic energy down to 0. So his initial kinetic energy is converted to potential energy (of s = 1.2 m) and the work done by snow:

`E_k = E_p + W_s`

`103500 = mgs + W_s`

`W_s = 103500 - mgs = 103500 - 82*1.2*9.8 = 101536 J`

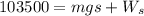
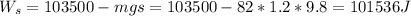
b) As work is the product of force over distance s = 1.2m, we can calculate the average force exerted on him as:

`F = W_s / s = 101536 / 1.2 = 84613 N`

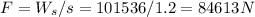
c) His potential energy when jumping off from the aircraft at height h = 390 m is

E = mgh = 82*9.8*390 = 313404 J

As he reaches the snow, air resistance has done some work on him and reduces his mechanical energy to 102500 J, so that work must be:

313404 - 102500 = 210904 J