Question

Quadrilateral CAMP below is a rhombus. the length PQ is (x+2) units, and the length of QA is (3x-14) units. Which statements best explains why the equation x+2 = 3x-14 can be use to find x?

Answer 1

Q cuts the diagonal PA into 2 equal halves, since the diagonals of rhombus meet at right angles.

The value of x is 8.

Explanation:

Given that Quadrilateral CAMP below is a rhombus. the length PQ is (x+2) units, and the length of QA is (3x-14) units

From the given Q is the middle point, which cut the diagonal PA into 2 equal halves.

By the definition of rhombus, diagonals meet at right angles.

Implies that PQ = QA

x+2 = 3x - 14

x-3x=-14-2

-2x=-16

2x = 16

dividing by 2 on both sides, we will get,

`x =(16)/(2)`

∴ x=8

Since Q cuts the diagonal PA into 2 equal halves, since the diagonals of rhombus meet at right angles we can equate x+2 = 3x-14 to find the value of x.

The line segment
`\overrightarrow{PA}=\overrightarrow{PQ}+\overrightarrow{QA}`

`\overrightarrow{PA}=x+2+3x-14`

`=4x-12`

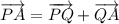
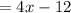
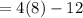`=4(8)-12` ( since x=8)

`=32-12`

`=20`

∴
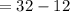
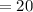
`\overrightarrow{PA}=20` units