Answer:
The number of surveys needed to be collected is 152.
Explanation:
The (1 - α)% confidence interval for population proportion p is:
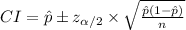
The margin of error for this interval is:
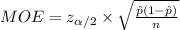
The information provided is:
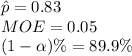
Compute the critical value of z for 89.9% confidence level as follows:
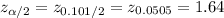
*Use a z-table.
Compute the sample size value as follows:
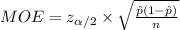
![n=[(z_(\alpha/2)* √(\hat p(1-\hat p)))/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/wb45wl5kvzkvb20txtpquood16fri70n9o.png)
![=[(1.64* √(0.83(1-0.83)))/(0.05)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/hzsp4slxmfwg2qtltwckbyv936zwrp7n7n.png)
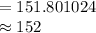
Thus, the number of surveys needed to be collected is 152.