Answer:
Hello your question ls not complete here is the missing equation and question
U ( c₁c₂ ) =
 ( c₁ )
( c₁ )
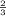 + α
+ α
 ( c₂ )
( c₂ )
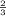
Derive the budget constraint that the person faces
ANSWER : c1 +
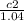 = 35000 +
= 35000 +
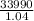
Step-by-step explanation:
period 1 income ( y1 ) = $35000
period 2 income ( y2 ) = $33990
interest rate = 3% = 0.03
utility ( c1, c2 ) =
 ( c1 )
( c1 )
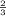 + α
+ α
 ( c2 )
( c2 )
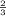
Deriving The budget constraint that the person faces
saving ( s ) = y1 - c1
c2 = ( 1 + r ) ( y1 - c1 ) + y2
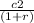 = y1 - c1 +
= y1 - c1 +
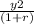
present value of consumption = present value of income
c1 +
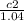 = 35000 +
= 35000 +
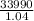
This is the derived equation