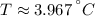Question

Between 0°C and 30°C, the volume V ( in cubic centimeters) of 1 kg of water at a temperature T is given approximately by the formula: V = 999.87 − 0.06426T + 0.0085043T² − 0.0000679T³ Find the temperature at which water has its maximum density.

Answer 1

`T \approx 3.967\,^(\textdegree)C`

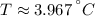
Explanation:

The density of water is given by the following definition:

`\rho = (m)/(V(T))`

`\rho = (1000\,g)/(999.870.06426\cdot T + 0.0085043\cdot T^(2)-0.0000679\cdot T^(3))`

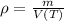
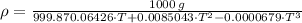
The density is maximum when volume is minimum, which can be found by First and Second Derivative Tests:

First Derivative

`V' = -0.06426 +0.0170086\cdot T -0.0002037\cdot T^(2)`

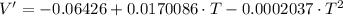
Second Derivative

`V'' = 0.0170086 - 0.0004074\cdot T`

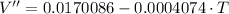
Critical values from the first derivative are:

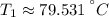`T_(1) \approx 79.531\,^(\textdegree)C` (absolute maximum) and
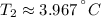`T_(2) \approx 3.967\,^(\textdegree)C` (absolute minimum).

The temperature at which water has its maximum density is:

`T \approx 3.967\,^(\textdegree)C`