Answer:

Explanation:
The density of water is given by the following definition:
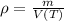
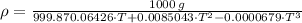
The density is maximum when volume is minimum, which can be found by First and Second Derivative Tests:
First Derivative
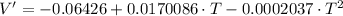
Second Derivative
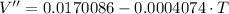
Critical values from the first derivative are:
 (absolute maximum) and
(absolute maximum) and
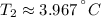 (absolute minimum).
(absolute minimum).
The temperature at which water has its maximum density is:
