The perimeter of the triangle is 15.4 units.
Explanation:
The triangle has vertices at (-1,5), (4,2), and (0,0).
To find the perimeter of the triangle, you need to find the distance of the three points which is the length of the three sides of the triangle.
Let us consider the points as A (-1,5) and B (4,2) and C (0,0).
The distance formula is given by :
⇒

Distance of AB :
A (-1,5) ⇒ (x1,y1)
B (4,2) ⇒ (x2,y2)
⇒
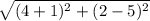
⇒

⇒
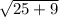
⇒
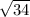
⇒ 5.8
∴ The length of the side AB of the triangle is 5.8 units.
Distance of BC :
B (4,2) ⇒ (x1,y1)
C (0,0) ⇒ (x2,y2)
⇒
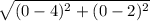
⇒
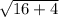
⇒
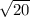
⇒ 4.5
∴ The length of the side BC of the triangle is 4.5 units.
Distance of CA :
C (0,0) ⇒ (x1,y1)
A (-1,5) ⇒ (x2,y2)
⇒
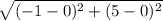
⇒
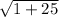
⇒
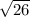
⇒ 5.1
∴ The length of the side CA of the triangle is 5.1 units.
Now, the perimeter of the triangle is given by :
Perimeter = Sum of the lengths of all three sides of the triangle.
⇒ 5.8 + 4.5 + 5.1
⇒ 15.4 units.
∴ The perimeter of the triangle is 15.4 units.