Question

Table : Alpo McBurgers

Alpho Cans Consumed per Day Total utility(Units of utility) McBurgers Consumed per Day Total utility(Units of utility)
0 0 0 0
1 7 1 16
2 13 2 28
3 16 3 36
4 17 4 40
1. Refer to the table with Alpo and McBurgers, if the price of one can of Alpo is $0.50 and the price of each McBurger is $1, which of the following would Ms. Tightwad, a utility-maximizing consumer, buy with her $4?
a. 4 McBurgers
b. 3 McBurgers and 2 cans of Alpo
c. 2 McBurgers and 4 cans of Alpo
d. 1 McBurger and 6 cans of Alpo

Answer 1

b. 3 McBurgers and 2 cans of Alpo

Step-by-step explanation:

If the goal is to maximize utility, Ms. Tightwad should look into purchasing the combination that yields the highest utility.

a. 4 McBurgers, 0 Alpo cans:

`U_a = 40`

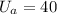
b. 3 McBurgers, 2 Alpo cans:

`U_b = 36+13 = 49`

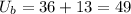
c. 2 McBurgers, 4 Alpo cans:

`U_c = 28+17 = 45`

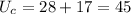
d. 1 McBurger, 6 Alpo cans (assume marginal utility stays constant after the 4th can):

`U_d = 16+17+2 = 35`

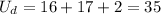
Since option b. yields the highest utility, she should buy 3 McBurgers and 2 cans of Alpo