Answer:
The speed of 65 mph is an outlier in the distribution of the player's serve speeds
Explanation:
We are given the following information in the question:
Mean, μ = 100 mph
Standard Deviation, σ = 10 mph
Formula:

Outlier on basis of z-score:
- Any z-score greater than 3 or less than -3 is considered to be an outlier.
- This rule of thumb is based on the empirical rule.
Calculation of z-score:
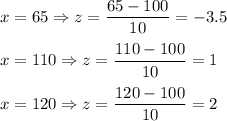
Thus, the speed of 65 mph is an outlier in the distribution of the player's serve speeds as the corresponding z-score is less than -3.