Question

Susan's 12.0 kg baby brother Paul sits on a mat. Susan pulls the man across the floor using a rope that is angled 30 degree above the floor. The tension is a constant 29.0 N and the coefficient of friction is 0.210. Use work and energy to find Paul's speed after being pulled 2.90 m.

Answer 1

Paul speed after being pulled 2.9 m is 2.68m/s.

Step-by-step explanation:

The work energy theorem, change in kinetic energy of the object from initial position to the final position is equal to the work done on the object ie when the force is applied on the object the object changes its position and work is done on the object.

According to the law of conservation of energy ,

ΔE = W, eqn 1

where ΔE is the change in object energy

W is the all the work done on the object.

Work done is written as W =F dcosθ

Where F is the force,

d is the distance,

θ is the angle between the force and displacement vector.

From the figure given below,

The work of friction is given by W₁ = F₁ d cos180°

The work of pulling force is given by W₂ =F₂ dcos 30°

Change in object energy ΔE = mv²/2.

Applying Newton first law along Y axis,

Fsin30° + N =mg

Normal force N =mg - Fsin30°

Frictional Force F₁ =μN =μ(mg - Fsin30°)

Substituting in eqn 1

mv²/2 = F₂ dcos 30°+ μ(mg - Fsin30°)d cos180°

=
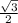`(√(3) )/(2)` F₂ d - μ(mg -
`(F)/(2)`)d

v² =
`√(3)`
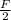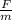`(F)/(m)`d - 2μgd +

here m = 12 kg,

d = 2.9 m.

μ = 0.21

F = 29 N

Sub all values,

v² = 7.2

v = 2.68m/s

Paul speed after being pulled 2.9 m is 2.68m/s.