Question

The Rocky Mountain district sales manager of Rath Publishing Inc., a college textbook publishing company, claims that the sales representatives make an average of 37 sales calls per week on professors. Several reps say that this estimate is too low. To investigate, a random sample of 41 sales representatives reveals that the mean number of calls made last week was 40. The standard deviation of the sample is 5.6 calls. Using the 0.025 significance level, can we conclude that the mean number of calls per salesperson per week is more than 37? H0: μ ≤ 37 H1: μ > 37 Compute the value of the test statistic. (Roun

Answer 1

We conclude that the mean number of calls per salesperson per week is more than 37.

Explanation:

We are given that the Rocky Mountain district sales manager of Rath Publishing Inc., a college textbook publishing company, claims that the sales representatives make an average of 37 sales calls per week on professors.

To investigate, a random sample of 41 sales representatives reveals that the mean number of calls made last week was 40. The standard deviation of the sample is 5.6 calls.

Let
`\mu` = true mean number of calls per salesperson per week.

SO, Null Hypothesis,
`H_0` :
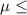`\mu \leq` 37 {means that the mean number of calls per salesperson per week is less than or equal to 37}

Alternate Hypothesis,
`H_A` :
`\mu` > 37 {means that the mean number of calls per salesperson per week is more than 37}

The test statistics that will be used here is One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

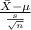where,
`\bar X` = sample mean number of calls made last week = 40

s = sample standard deviation = 5.6 calls

n = sample of sale representatives = 41

So, test statistics =
`(40-37)/((5.6)/(√(41) ) )` ~
`t_4_0`

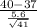= 3.43

Hence, the value of test statistics is 3.43.

Now at 0.025 significance level, the t table gives critical value of 2.021 at 40 degree of freedom for right-tailed test. Since our test statistics is more than the critical value of t as 3.43 > 2.021, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the mean number of calls per salesperson per week is more than 37.