Question

In the diagram below, quadrilateral ABCD is inscribed in a circle. What is the measure of angle D?

Answer 1

110

Explanation:

The top angles are congruent and the bottom angles are congruent

Answer 2

Given:

In the circle P, ABCD is inscribed quadrilateral.

And, ∠DAB = 110°, ∠ABC = 72°

To find the value of ∠ADC.

Theorem:

A quadrilateral can be inscribed in a circle if and only if the opposite angles are supplementary [ sum of the opposite angles will be 180°]

According to the theorem,

`\angle ABC+\angle ADC = 180^(\circ)`

`\angle ADC +72^(\circ) = 180^(\circ)`

`\angle ADC = 180^(\circ)-72^(\circ)`

`\angle ADC = 108^(\circ)`

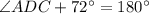
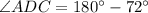
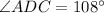
Hence,

The value of ∠ADC is 108°.

Hence, Option b is the correct answer.