Answer:
tan(S) =
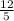
Explanation:
Hi there!
We are given ΔRST, where ST=5, RT=12, and RS=13
We want to find the tangent of angle S (the notation tan(S) means "tangent of angle S")
In trigonometry, tangent refers to the ratio of the opposite side/adjacent side.
The opposite side is the side that is opposite to the angle that we are referencing (in this case, angle S); in this case, that side is RT, which is 12
The adjacent side is the leg that is adjacent to the opposite side; in this case, that side is ST, which we were given as 5
Therefore, tan(S) will be
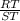 , or
, or
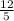 .
.
Hope this helps!