Question

There are two peice pf gold and silver alloy. The ratio between the gold and silver in the first piece is 2:3, in the second peice 3:7. If we want to have 8 gram of gold and silver alloy with gold-silver ratio 5:11 how much of each peice of alloy is needed.

Answer 1

• 1 grams of one of the alloy; and
• 7 grams of the other corresponding alloy.

Explanation:

The ratio between the gold and silver in the first piece = 2:3

The ratio between the gold and silver in the second piece =3:7

The ratio in the mixture = 5:11

We want to have 8 gram of the new mixture.

Let the gram of alloy taken from the first piece=x

Therefore: gram of alloy would be taken from the second piece=(8-x)

This gives:

`(2)/(5)x+ (3)/(10)(8-x)=(5)/(16)*8`

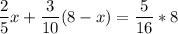
We simplify the equation above for the value of x.

`(2x)/(5)+ (3(8-x))/(10)=(5)/(2) \\(4x+24-3x)/(10)=(5)/(2)\\(x+24)/(10)=(5)/(2)\\2x+48=50\\2x=50-48\\2x=2\\x=1`

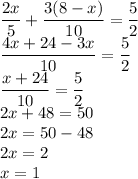
Therefore to create 8 gram of gold and silver alloy with gold-silver ratio 5:11, we take 1 grams of one of the alloy and 7 grams of the other alloy.