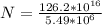Answer:
The approximate number of decays this represent is

Step-by-step explanation:
From the question we are told that
The amount of Radiation received by an average american is

The source of the radiation is
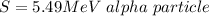
Generally
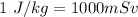
Therefore

Also
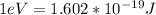
Therefore
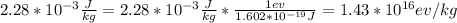
An Average american weighs 88.7 kg
The total energy received is mathematically evaluated as

Cross-multiplying and making x the subject
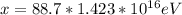
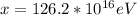
Therefore the total energy deposited is
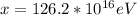
The approximate number of decays this represent is mathematically evaluated as
N =
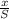
Where n is the approximate number of decay
Substituting values