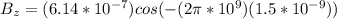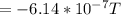Question

A plane monochromatic radio wave (? = 0.3 m) travels in vacuum along the positive x-axis, with a time-averaged intensity I = 45.0 W/m2. Suppose at time t = 0, the electric field at the origin is measured to be directed along the positive y-axis with a magnitude equal to its maximum value. What is Bz, the magnetic field at the origin, at time t = 1.5 ns? Bz = I got .04800 but that answer didnt work.

Answer 1

The magnetic field
`B_Z`
`= - 6.14*10^(-7) T`

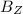
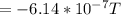
Step-by-step explanation:

From the question we are told that

The wavelength is
`\lambda = 0.3m`

The intensity is
`I = 45.0W/m^2`

The time is
`t = 1.5ns = 1.5 *10^(-9)s`

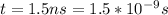
Generally radiation intensity is mathematically represented as

`I = (1)/(2) c \epsilon_o E_o^2`

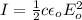
Where c is the speed of light with a constant value of
`3.0 *10^8 m/s`

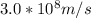
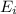`E_i` is the electric field

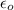`\epsilon_o` is the permittivity of free space with a constant value of
`8.85*10^(-12) C^2 /N \cdot m^2`

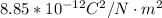
Making
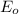`E_o` the subject of the formula we have

`E_i = \sqrt{(2I)/(c \epsilon_0) }`

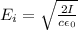
Substituting values

`E_i = \sqrt{(2* 45 )/((3*10^8 * (8.85*10^(-12)) )) }`

`= 184.12 \ V/m`

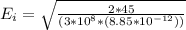
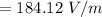
Generally electric and magnetic field are related by the mathematical equation as follows

`(E_i)/(B_i) = c`

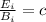
Where
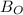`B_O` is the magnetic field

making
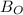`B_O` the subject

`B_i = (E_i)/(c)`

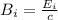
Substituting values

`B_i = (184.12)/(3*10^8)`

`= 6.14 *10^(-7)T`

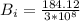
Next is to obtain the wave number

Generally the wave number is mathematically represented as

`n = (2 \pi )/(\lambda )`

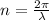
Substituting values

`n = (2 \pi)/(0.3)`

`= 20.93 \ rad/m`

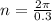
Next is to obtain the frequency

Generally the frequency f is mathematically represented as

`f = (c)/(\lambda)`

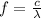
Substituting values

`f = (3 *10^8)/(0.3)`

`= 1*10^(9) s^(-1)`

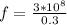
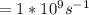
Next is to obtain the angular velocity

Generally the angular velocity
`w` is mathematically represented as

`w = 2 \pi f`

`w = 2 \pi (1* 10^9)`

`= 2 \pi * 10^9 rad/s`

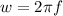
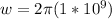
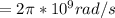
Generally the sinusoidal electromagnetic waves for the magnetic field B moving in the positive z direction is expressed as

`B_z = B_i cos (nx -wt)`

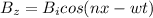
Since the magnetic field is induced at the origin then the equation above is reduced to

`B_z = B_i cos (n(0) -wt) = B_i cos ( -wt)`

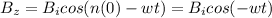
x =0 because it is the origin we are considering

Substituting values

`B_z = (6.14*10^(-7)) cos (- (2 \pi * 10^(9))(1.5 *10^(-9)))`

`= - 6.14*10^(-7) T`