Answer:
f(16)=162
Explanation:
-In a geometric sequence, the quotient between any tow consecutive numbers is called the common ratio,r:
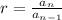
Given that f(3)=32 and f(9)=72, we can find the common ratio as below:
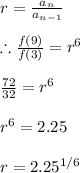
#We substitute and use the same formula to find the nth term:
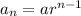
let f(3) be a(the first term):
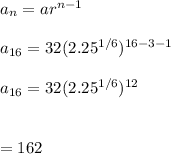
Hence, f(16)=162