Question

The population of Thomasville was 2,460 in 2006, and is growing at an annual rate of 3.5%. This can be modeled by the exponential function f(x) = 2460(1.035) ^x.

How does the function change over the interval from x=2 to x=3?
A. f(x) increases by 3.5%
B. f(x) decreases by 3.5%
C. f(x) increases by a factor of 2460
D. f(x) decreases by a factor of 2460
​

Answer 1

A. f(x) increases by 3.5%

Explanation:

Given:

City of Thomasville.

Population in 2006,
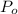`P_o` = 2460

Exponential function, f(x) = 2460(1.035) ^x ...equivalent to
`P=P_o(1+r)^t`

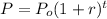
Function change at x = 2, 3

According to the question:

Plugging the values of x= 2 and x=3 we have to find the population at different x.

So,

At x= 2 At x=3

⇒
`P_2=P_o(1+r)^t` ⇒
`P_3=P_o(1+r)^t`

⇒
`P_2=2460(1.035)^x` ⇒
`P_3=2460(1.035)^x`

⇒
`P_2=2460(1.035)^2` ⇒
`P_3=2460(1.035)^3`

⇒
`P_2=2622.4` ⇒
`P_3=2707.7`

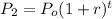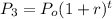
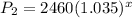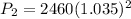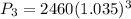
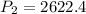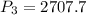
Percent change :

⇒
`\triangle \% =(Final\ value -Initial\ value)/(Initial\ value) * 100`

⇒
`\triangle \% = ((P_3-P_2))/(P_2) * 100`

⇒
`\triangle \% = ((2707.7-2622.4))/(2622.4) * 100`

⇒
`\triangle \% = 3.5`

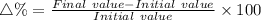
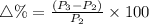
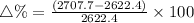
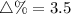
So,

The function f(x) increases by 3.5% option A is the right choice.