Question

The magnetic field within a long, straight solenoid with a circular cross section and radius r is increasing at a rate of dbdt. part a what is the rate of change of flux through a circle with radius r1 inside the solenoid, normal to the axis of the solenoid, and with center on the solenoid axis? express your answer in terms of the variables r, b, r1, and appropriate constants.

Answer 1

`(d\Phi_B)/(dt)=(d(\pi r_1^2B))/(dt)=\pi r_1^2(dB)/(dt)`

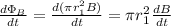
Step-by-step explanation:

To calculate the rate of change of the flux we have to take into account that the magnetic flux is given by

`\Phi_B=\vec{B}\cdot \vec{A}`

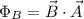
in this case the direction of B is perpendicular to the direction of A. Hence

`\Phi_B=BA`

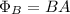
and A is the area of a circle:

`A=\pi r^2`

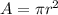
in this case we are interested in the flux of a area of a lower radius r1. Hence

`A=\pi r_1^2`

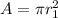
Finally, the change in the magnetic flux will be

`(d\Phi_B)/(dt)=(d(\pi r_1^2B))/(dt)=\pi r_1^2(dB)/(dt)`

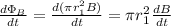
hope this helps!!