Question

The stopping distance (s) of a car varies directly as the square of its speed (v). If a car traveling 20 mph requires 60 ft to stop, find the stopping distance for a car traveling 40 mph. Round to the nearest tenth.

Answer 1

The stopping distance for a car traveling 40 mph is 240 feet.

Explanation:

We are given the following in the question:

The stopping distance (s) of a car varies directly as the square of its speed (v)

`s\propto v^2`

Removing the sign of proportionality and adding constant of proportionality, we get

`s = kv^2`

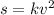
where k is constant of proportionality.

Now, when s = 60 feet, v = 20 mph

Putting values, we get,

`60 = k(20)^2\\\\k = (60)/(400) = 0.15`

Putting value of k in the equation, we get,

`s = 0.15v^2`

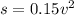
We have to find the stopping distance for a car traveling 40 mph.

`s = 0.15(40)^2 = 240\text{ feet}`

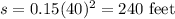
Thus, the stopping distance for a car traveling 40 mph is 240 feet.