Given:
The given polynomial is:
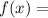

To find the roots of the given polynomial.
To find the roots we have to take

So,
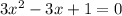
Formula
By quadratic formula, the root of the equation
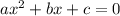 is,
is,
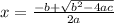 and
and
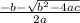
Now,
Putting,
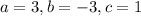 we get,
we get,
 and
and
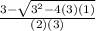
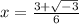 and
and
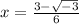
Hence,
The values of the roots of the given polynomial are
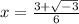 and
and
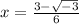
Hence, Option A and F are the correct answer.