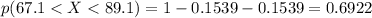Question

The score on an exam from a certain MAT 112 class, X, is normally distributed with μ=78.1 and σ=10.8.

NOTE: Assume for the sake of this problem that the score is a continuous variable. A score can thus take on any value on the continuum. (In real life, scores are often treated as if they were continuous values but are actually discrete in most cases.)

(a) Write the event ''a score less than 67.1'' in terms of X:
.

(b) Find the probability of this event:
(c) Find the probability that a randomly chosen score is greater than 89.1:
.

(d) Find the probability that a randomly chosen score is between 67.1 and 89.1:

Answer 1

a)
`X<67.1`

b) 0.1539

c) 0.1539

d) 0.6922

Explanation:

a)

In this problem, the score on the exam is normally distributed with the following parameters:

`\mu=78.1` (mean)

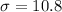`\sigma = 10.8` (standard deviation)

We call X the name of the variable (the score obtained in the exam).

Therefore, the event "a student obtains a score less than 67.1) means that the variable X has a value less than 67.1. Mathematically, this means that we are asking for:

`X<67.1`

And the probability for this to occur can be written as:

`p(X<67.1)`

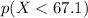
b)

To find the probability of X to be less than 67.1, we have to calculate the area under the standardized normal distribution (so, with mean 0 and standard deviation 1) between
`z=-\infty` and
`z=Z`, where Z is the z-score corresponding to X = 67.1 on the s tandardized normal distribution.

The z-score corresponding to 67.1 is:

`Z=(67.1-\mu)/(\sigma)=(67.1-78.1)/(10.8)=-1.02`

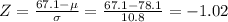
Therefore, the probability that X < 67.1 is equal to the probability that z < -1.02 on the standardized normal distribution:

`p(X<67.1)=p(z<-1.02)`

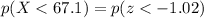
And by looking at the z-score tables, we find that this probability is:

`p(z<-1.02)=0.1539`

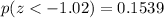
And so,

`p(X<67.1)=0.1539`

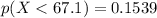
c)

Here we want to find the probability that a randomly chosen score is greater than 89.1, so

`p(X>89.1)`

First of all, we have to calculate the z-score corresponding to this value of X, which is:

`Z=(89.1-\mu)/(\sigma)=(89.1-78.1)/(10.8)=1.02`

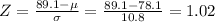
Then we notice that the z-score tables give only the area on the left of the values on the left of the mean (0), so we have to use the following symmetry property:

`p(z>1.02) =p(z<-1.02)`

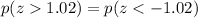
Because the normal distribution is symmetric.

But from part b) we know that

`p(z<-1.02)=0.1539`

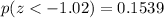
Therefore:

`p(X>89.1)=p(z>1.02)=0.1539`

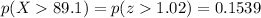
d)

Here we want to find the probability that the randomly chosen score is between 67.1 and 89.1, which can be written as

`p(67.1<X<89.1)`

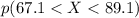
Or also as

`p(67.1<X<89.1)=1-p(X<67.1)-p(X>89.1)`

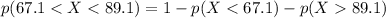
Since the overall probability under the whole distribution must be 1.

From part b) and c) we know that:

`p(X<67.1)=0.1539`

`p(X>89.1)=0.1539`

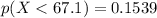
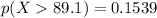
Therefore, here we find immediately than:

`p(67.1<X<89.1)=1-0.1539-0.1539=0.6922`