Question

Which type of function describes her total savings after m months and why?

Answer 1

A.

Explanation:

I would advise finding the difference between 300 and 200 and 450 and 300:

`300-200=100\\450-300=150`

We can eliminate C and D since she saves 100 the first month and 150 the second month.

The next step would be to find the increase every month:

`(Final value)/(initial value)=x\\\\(300)/(200)=1.5 \\\\(450)/(300) = 1.5`

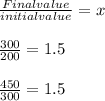
If we would write the increase as a function, we would get:

`y= 1.5x`

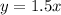
we can check this by substituting values:

`y=1.5*200\\y=300\\\\\\y=1.5*300\\y=450`

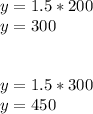
An exponential function looks like this:

`y= a^x`

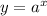
A linear function looks like this:

`y=mx+b`

Our m is 1.5, a linear increase by 150% and our b is 0, which can be written like:

`y=1.5x+0\\y=1.5x`

Therefore our function resembles a linear function more than an exponential function, eliminating answer B.