Given:
∠1 = 2x+6 ans ∠2= -x+24
To find the values of ∠1 and ∠2.
Formula:
The values of the vertical angles are always equal.
Here,
∠1 and ∠2 are vertical angles.
So, by this condition,
∠1=∠2
or,
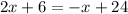
or,
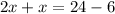 [ Taking all the variables in one side and all the constant in other side]
[ Taking all the variables in one side and all the constant in other side]
or,
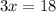
or,
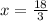
or,
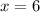
So,
∠1 =
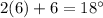
∠2 =
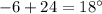
Hence,
The values of ∠1 and ∠2 are 18°.