Question

A company has determined that when x hundred dulcimers are built, the average cost per dulcimer can be estimated by C(x)=0.3x^(2)-2.7x+7.775, where C(x) is hundreds of dollars. What is the mimimum average cst per dulcimer and how many dulcimers should be built to achieve that minimum?

Answer 1

4.5 hundreds dulcimers should be build to achieve the minimum average cost per dulcimer $ 1.7 hundreds.

Explanation:

The average cost per dulcimer can be estimated by

C(x)=0.3x² -2.7x+7.775

where C(x) is hundreds of dollar, x hundred dulcimers are built.

C(x)=0.3x² -2.7x+7.775

Differentiating with respect to x

C'(x)=0.6x-2.7

Again differentiating with respect to x

C''(x)=0.6

For maximum or minimum C'(x)=0

0.6x-2.7=0

⇒0.6x=27

`\Rightarrow x=\frac {2.7}{0.6}`

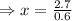
⇒ x= 4.5

Now
`C''(x)|_(x=4.5)= 0.6>0`

Since at x= 4.5 , C''(x)>0, So, the average cost per dulcimer is minimum.

C(4.5)= 0.3(4.5)²-2.7×4.5 +7.775×

=1.7

4.5 hundreds dulcimers should be build to achieve the minimum average cost per dulcimer $ 1.7 hundreds.