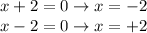Question

Determine the zeroes of 10x2−5=35

Answer 1

x = +2, x = -2

Explanation:

The equation to solve in this problem is

`10x^2-5=35`

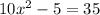
The first step we do is to subtract 35 on both sides of the equation, so we get:

`10x^2-5-35=0\\10x^2-40=0`

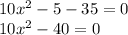
Now we simplify the equation by dividing both terms by 10:

`(10x^2-40)/(10)=0\\x^2-4=0`

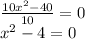
Now we observe that the term on the left is the difference between two squares, so it can be rewritten using the property:

`a^2-b^2=(a+b)(a-b)`

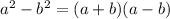
Where here,

a = x

b = 2

So we can rewrite the equation as:

`x^2-4=0\\(x+2)(x-2)=0`

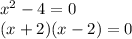
And this equation is zero when either one of the two factors is zero, so the two solutions are:

`x+2=0\rightarrow x=-2\\x-2=0 \rightarrow x=+2`