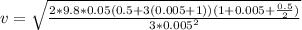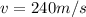Question

Consider the ballistic pendulum we discussed in class, where a bullet of mass mb = 5 g is fired into a block of mass mB = 1 kg and gets lodged into the block. The bullet and block are then allowed to swing upward, reaching a final height of h. Here, however, instead of the block of being suspended by masses strings it is suspended by two thin rods of mass M = 0.5 kg and length 1 m.

(a) What is conserved in the collision, be specific?
(b) What is the angular-speed, w, of the ballistic pendulum right after the collision?
(c) To what height h will the ballistic pendulum swing up to?
(d) If the ballistic pendulum swing up to a height of h 5 cm, what is the initial speed of the bullet?

Answer 1

Complete Question

The diagram fro this question is shown on the first uploaded image

Answer:

a

The Answer is Angular Momentum

b

The angular velocity is

`w = (3m_b v)/(l(M + 3(m_B +m_b)))`

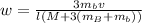
c

The Maximum height of ballistic is

`h = (3 m_b^2 v^2 )/(2 [M + 3(m_b + m_B) ] ( m_B + m_b + (M)/(2) )g )`

d The initial velocity is

`v= 240 m/s`

Step-by-step explanation:

From the question we are told that

The mass of the bullet is
`m_b = 5g = (5)/(1000) = 0.005kg`

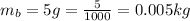
The mass of block
`m_B = 1kg`

The final height is h

The mass of the rod is
`M =0.5kg`

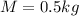
The length of the rod is
`L = 1m`

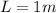
a

The free body diagram of this question is shown on the second and third uploaded image

From the diagram we see that

The rod is hinged

This tell us that the net force is not zero

Secondly it tells us that the net torque zero and if the net torque is zero the angular momentum of the system is conserved

Because angular momentum is mathematically related to torque as follows

`(dl)/(dt) = T`

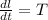
Here dl/dt is the change angular momentum with time and since in this question torque is zero then there is no change in angular momentum with time

b

Since angular momentum is conserved then the

angular momentum before collision = angular momentum after collision

Generally angular momentum is mathematically represented as

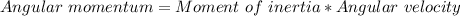
`Angular \ momentum = Moment \ of \ inertia * Angular \ velocity`

angular momentum before collision =
`m_b * v * l`

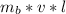
angular momentum after collision =
`Iw + I_B w+ I_bw`

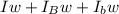
Where
`I` is the moment of inertia and for a rod the moment of inertia is mathematically represented as

`I = (M l^3)/(3)`

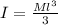
The moment of inertia for block is

`I_B =m_B l^2`

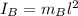
The moment of inertia for bullet

`I_b =m_b l^2`

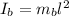
Substituting this into the equation for conservation of momentum

`m_b * v * l = Iw + m_B l^2 + m_b l^2w`

`m_b \ v \ l = (M l^2)/(3)w + m_B l^2 w + m_b l^2 w`

`m_b \ v \ l = (M + 3 (m_B + m_b))/(3) l^2 w`

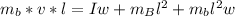
Making angular velocity the subject of the formula

`w = (3m_b v)/(l(M + 3(m_B +m_b)))`

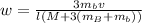
c

Looking at the third diagram we see that the

Mass of the bullet + mass of block was rises to height h

but the mass of the rod just raise to a height of
`(h)/(2)`

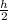
According to the law of conservation of energy

The total rotational kinetic energy in the system = Total potential energy in the system

Therefore mathematically

`(1)/(2) I_Tw^2 = [m_B + m_b ]gh + mg (h)/(2)`

Where
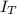`I_T` is the total moment of inertia for block ,bullet and rod and this mathematically evaluated as

`I_T = (Ml^2)/(2) + m_B l^2 + m_b L^2`

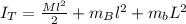
Substituting this into the equation for energy conservation

`(1)/(2)[ (Ml^2)/(2) + m_B l^2 + m_b L^2]w^2 = [m_B + m_b ]gh + mg (h)/(2)`

`(1)/(2)[ (Ml^2)/(2) + m_B l^2 + m_b L^2][(3m_b v)/(l(M + 3(m_B +m_b)))] = hg[m_B + m_b + (M)/(2) ]`

Making h the subject of the formula

`h = (3 m_b^2 v^2 )/(2 [M + 3(m_b + m_B) ] ( m_B + m_b + (M)/(2) )g )`

d

Making the initial velocity of the bullet v the subject of the formula

`v = \sqrt{(2gh(M + 3 (m_b + m_B )) (m_B + m_b + (M)/(2) ))/(3 m_b^2) }`

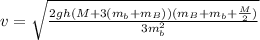
Given that
`h = 5cm = (5)/(100) =0.05m`

Substituting values into the equation for initial velocity

`v = \sqrt{(2 * 9.8 * 0.05 (0.5+3(0.005 + 1 )) (1 + 0.005 + (0.5)/(2) ))/(3 * 0.005^2) }`

`v= 240 m/s`