Question

You have been asked to determine where a water works should be built along a river between Chesterville and Denton to minimize the total cost of the project. The pipe to Chesterville costs $3000 per mile and the pipe to Denton costs $7000 per mile.

a. Find the length of each pipe so that the total cost is a minimum.
b. What is the cost?

Answer 1

The pipe to Chesterville has a length of 8.37 miles.

The pipe to Denton has a length of 5.46 miles.

The total cost is $63,330.

Explanation:

The question is incomplete: the attached picture is needed to understand the optimization problem.

Being Pc the length of the pipe to Chesterville and Pd the length pipe to Denton, we can express them in function of x, using the Pyhtagorean theorem:

`P_c=√(3^2+x^2)\\\\P_d=\sqrt{5^2+(10-x)^2`

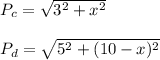
The cost of the project is the function to be optimized and can be expressed as:

`C=3,000P_c+7,000P_d\\\\\\C=3,000√(9+x^2)+7,000√(25+(10-x)^2)`

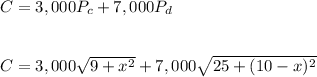
To optimize this function, we can derive and equal to 0.

`(dC)/(dx)=3,000(d)/(dx)(√(9+x^2))+7,000(d)/(dx)(√(25+(10-x)^2))\\\\\\(dC)/(dx)=3,000((1)/(2)(x^2+9)^(0.5-1)*2x)+7,000((1)/(2)(25+(10-x)^2)^(0.5-1)*(-2(x-10))\\\\\\(dC)/(dx)=3,000(x)/(√(x^2+9))+7,000(x-10)/(√(25+(10-x)^2))=0\\\\\\3,000(x)/(√(x^2+9))=-7,000(x-10)/(√(25+(10-x)^2))\\\\\\3,000x(25+(x-10)^2)^(0.5)=-7,000(x-10)(x^2+9)^(0.5)\\\\\\`

`(3,000x^2)(25+(x-10)^2)=(-7,000(x-10))^2(x^2+9)\\\\\\3,000^2x^2(25+x^2-20x+100)=7,000^2(100-20x+x^2)(x^2+9)\\\\\\3,000^2(x^4-20x^3+125x^2)=7,000^2(100x^2+900-20x^3-180x+x^4+9x^2)\\\\\\3,000^2(x^4-20x^3+125x^2)=7,000^2(x^4-20x^3+109x^2-180x+900)`

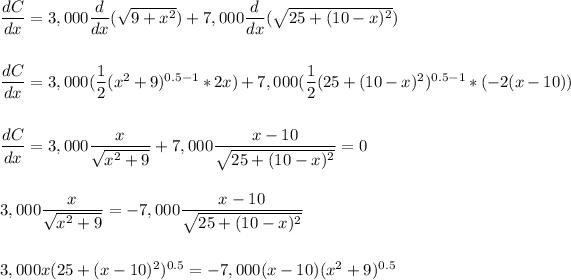
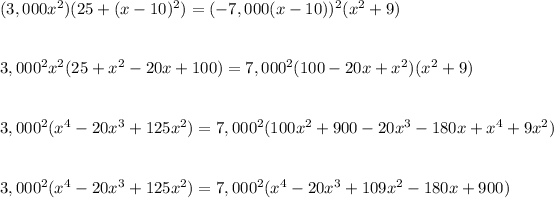
If we graph this polynomial, with x between its possible domain x=[0,10], we can see that it equal zero for x=7.817.

The lenghts of the pipes are:

`P_c=√(3^2+x^2)\\\\P_c=√(9+(7.817)^2)=√(9+61.1)=√(70.1)=8.37\\\\\\ P_d=√(5^2+(10-x)^2)\\\\P_d=√(25+(10-(7.817))^2)= √(25+2.183^2)= √(29.8)= 5.46`

We know the pipes length, but now we need to calculate the cost:

`C=3,000P_c+7,000P_d\\\\\\C=3,000*8.37+7,000*5.46\\\\C=25,110+38,220\\\\C=63,330`