Answer:
A, C, and D
Explanation:
The rate of change will simply be the slope of the line, which we can find by taking the change in y and dividing that by the change in x:
slope =
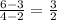
Thus, the slope is 3/2 = 1.5.
Since the slope remains constant throughout the graph, we know that A is correct. In addition because the points 0, 2, 4, and 6 are on the graph, the rate of change between any of the two points will still be the constant 1.5, making C and D correct as well.
So, we can choose A, C, and D.
Hope this helps!