Answer:
x = 3 and y = 2 or (3,2) in coordinate form
Explanation:
Given:
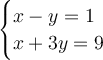
Solve by elimination of x-terms by multiplying either one of equations with -1:
For this, I choose to multiply -1 in first equation:
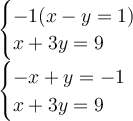
Then add both equations:
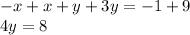
Divide both sides:
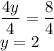
Next, substitute y = 2 in one of equations to solve for x:
For this, I choose to substitute y = 2 in the first equation:
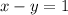
Substitute y = 2 in:

Add both sides by 2:
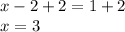
Hence, the solution is x = 3 and y = 2 or you can write as in coordinate form (3,2)
__________________________________________________________
First method is elimination method, I’ll demonstrate another method which is by using matrices to find the solutions.
Given:
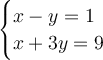
Write the system of equations in matrices form:
![\displaystyle \large{\left[\begin{array}{ccc}1&-1\\1&3\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}1\\9\end{array}\right]}](https://img.qammunity.org/2023/formulas/mathematics/high-school/v2l4s86g7a6le5lpyfghe7ai2ksu39xtag.png)
Let:
![\displaystyle \large{A=\left[\begin{array}{ccc}1&-1\\1&3\end{array}\right] }\\\displaystyle \large{X=\left[\begin{array}{ccc}x\\y\end{array}\right] \\\displaystyle \large{B = \left[\begin{array}{ccc}1\\9\end{array}\right] }](https://img.qammunity.org/2023/formulas/mathematics/high-school/pqsi71fi71tdnebtozu0397dzadgtes4xs.png)
From
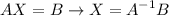 where:
where:
![\displaystyle \large{A^(-1)=(1)/(\det A) \left[\begin{array}{ccc}d&-b\\-c&a\end{array}\right] = (1)/(ad-bc) \left[\begin{array}{ccc}d&-b\\-c&a\end{array}\right] }](https://img.qammunity.org/2023/formulas/mathematics/high-school/h9o8vxv3ihoj7mohb9g4efhzsa55jce78t.png)
Find
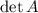 :
:

Therefore:
![\displaystyle \large{A^(-1) = (1)/(4)\left[\begin{array}{ccc}3&1\\-1&1\end{array}\right]}\\\therefore \displaystyle \large{X = (1)/(4)\left[\begin{array}{ccc}3&1\\-1&1\end{array}\right] \left[\begin{array}{ccc}1\\9\end{array}\right]}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ovtdxfuiai8kgqdkcq30dn5bgrev05384d.png)
Evaluate the matrices:
![\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}3(1)+1(9)\\-1(1)+1(9)\end{array}\right] }\\\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}3+9\\-1+9\end{array}\right] }\\\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}12\\8\end{array}\right]}\\\displaystyle \large{X= \left[\begin{array}{ccc}3\\2\end{array}\right] }\\\therefore \displaystyle \large{\left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}3\\2\end{array}\right]}](https://img.qammunity.org/2023/formulas/mathematics/high-school/d4cyp4jd3fiicwrviapdeo5vxka30dxqh4.png)
Therefore, the solution is x = 3 and y = 2