Question

Complete part (a) and part (b) given the following system of equations.

x-y=1
x + 3y =9
Write your answer.

Answer 1

x = 3 and y = 2 or (3,2) in coordinate form

Explanation:

Given:

`\displaystyle \large{\begin{cases} x-y=1 \\ x+3y=9 \end{cases}}`

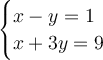
Solve by elimination of x-terms by multiplying either one of equations with -1:

For this, I choose to multiply -1 in first equation:

`\displaystyle \large{\begin{cases} -1(x-y=1) \\ x+3y=9 \end{cases}}\\\displaystyle \large{\begin{cases} -x+y=-1 \\ x+3y=9 \end{cases}}`

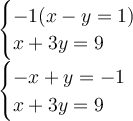
Then add both equations:

`\displaystyle \large{-x+x+y+3y=-1+9}\\\displaystyle \large{4y=8}`

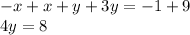
Divide both sides:

`\displaystyle \large{(4y)/(4) = (8)/(4)}\\\displaystyle \large{y=2}`

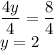
Next, substitute y = 2 in one of equations to solve for x:

For this, I choose to substitute y = 2 in the first equation:

`\displaystyle \large{x-y=1}`

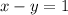
Substitute y = 2 in:

`\displaystyle \large{x-2=1}`

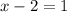
Add both sides by 2:

`\displaystyle \large{x-2+2=1+2}\\\displaystyle \large{x=3}`

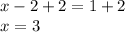
Hence, the solution is x = 3 and y = 2 or you can write as in coordinate form (3,2)

__________________________________________________________

First method is elimination method, I’ll demonstrate another method which is by using matrices to find the solutions.

Given:

`\displaystyle \large{\begin{cases} x-y=1 \\ x+3y=9 \end{cases}}`

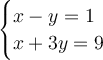
Write the system of equations in matrices form:

`\displaystyle \large{\left[\begin{array}{ccc}1&-1\\1&3\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}1\\9\end{array}\right]}`

Let:

`\displaystyle \large{A=\left[\begin{array}{ccc}1&-1\\1&3\end{array}\right] }\\\displaystyle \large{X=\left[\begin{array}{ccc}x\\y\end{array}\right] \\\displaystyle \large{B = \left[\begin{array}{ccc}1\\9\end{array}\right] }`

From
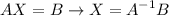`\displaystyle \large{AX=B \to X=A^(-1)B}` where:

`\displaystyle \large{A^(-1)=(1)/(\det A) \left[\begin{array}{ccc}d&-b\\-c&a\end{array}\right] = (1)/(ad-bc) \left[\begin{array}{ccc}d&-b\\-c&a\end{array}\right] }`

Find
`\displaystyle \large{\det A}`:

`\displaystyle \large{\det A = ad-bc = 3+1=4}`

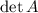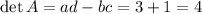
Therefore:

`\displaystyle \large{A^(-1) = (1)/(4)\left[\begin{array}{ccc}3&1\\-1&1\end{array}\right]}\\\therefore \displaystyle \large{X = (1)/(4)\left[\begin{array}{ccc}3&1\\-1&1\end{array}\right] \left[\begin{array}{ccc}1\\9\end{array}\right]}`

Evaluate the matrices:

`\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}3(1)+1(9)\\-1(1)+1(9)\end{array}\right] }\\\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}3+9\\-1+9\end{array}\right] }\\\displaystyle \large{X= (1)/(4)\left[\begin{array}{ccc}12\\8\end{array}\right]}\\\displaystyle \large{X= \left[\begin{array}{ccc}3\\2\end{array}\right] }\\\therefore \displaystyle \large{\left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}3\\2\end{array}\right]}`

Therefore, the solution is x = 3 and y = 2

Answer 2

(3,2)

Explanation:

Setting up equation so we can use substitution method

x - y = 1 , x + 3y = 9

step 1 set first equation equal to x by adding y to both sides so we can use the substitution method to solve the system of equations.

x = y + 1 , x + 3y = 9

now we can plug in ( or substitute hence substitution method ) the first equation into the second

Solving for y using the substitution method

x + 3y = 9

plug in x = y + 1

y + 1 + 3y = 9

combine like terms

4y + 1 = 9

subtract 1 from both sides

4y = 8

divide both sides by 4

y = 2

Now to find the value of x we plug in the value of y into one of the equations and solve for x.

Solving for x

x - y = 1

y = 2

x - 2 = 1

add 2 to both sides

x = 3

The solution would be (3,2)