Given:
Given that O is the center of the circle.
AB is tangent to the circle.
The measure of ∠AOB is 68° and we know that the tangent meets the circle at 90°
We need to determine the measure of ∠ABO.
Measure of ∠ABO:
The measure of ∠ABO can be determined using the triangle sum property.
Applying the property, we have;
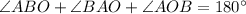
Substituting the values, we get;
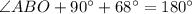
Adding the values, we have;

Subtracting both sides by 158, we get;

Thus, the measure of ∠ABO is 22°