Question

Given the function g(x) = -x^2+ 2x + 8, determine the average rate of change of

the function over the interval -3 < x < 2.

Answer 1

3

Explanation:

The average rate of change of g(x) in the closed interval [ a, b ] is

`(g(b)-g(a))/(b-a)`

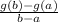
Here [ a, b ] = [ - 3, 2 ], thus

g(b) = g(2) = - 2² + 2(2) + 8 = - 4 + 4 + 8 = 8

g(a) = g(- 3) = - (- 3)² + 2(- 3) + 8 = - 9 - 6 + 8 = - 7

average rate of change =
`(8-(-7))/(2-(-3))` =
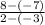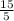`(15)/(5)` = 3