What's with the gratuitous pi s?
The rule is to preserve inequalities we can only multiply both sides by positive numbers, or non-negative numbers (zero ok) for ≤ and ≥ (but not < and >).
To clear the denominator, first we need all positive factors down there so we multiply by
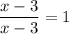
giving
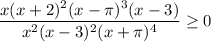
Everything in the denominator is positive now, so we can clear it, multiplying it on both sides. It vanishes on both sides.
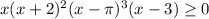
Again we can divide both sides by the positive factors, which are the squares, including (x-π)². We'll get zero when those factors are zero (and no zero denominator factor), so we have to remember to include x=0, x=-2, x=3 and x=π in the answer, but we eliminate 0 and 3 from this list because they give zero denominators.
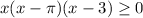
That's a lot easier to think about. When x is really negative we're multiplying three negative numbers, so a negative result.
When x is really big we're multiplying three positive numbers, again a positive result.
Between 0 and pi it's going to alternate.
<0 negative
0-3 positive
3-π negative
>π positive
Since zero is ok we can use ≤ or ≥ as appropriate, but we should also rule out anything that gives a zero denominator, as the truth value of 'undefined ≥ 0' is not really determined.
Answer: 0 < x < 3 or x ≥ π or x=-2
[I missed the x=-2 the first time around; sorry about that.]