Question

Triangle ABC has vertices A(-2, 3), B(0, 3), and C(-1,-1). Find the coordinates of the image after a reflection over the

x-axis.
​

Answer 1

A - (-2,-3)

B - (0,-3)

C - (-1,1)

Explanation:

Answer 2

Given:

Given that the triangle ABC has vertices A(-2,3), B(0,3) and C(-1,-1).

We need to determine the coordinates of the image after a reflection over the x - axis.

Let A'B'C' denote the coordinates of the triangle after a reflection over the x - axis.

Coordinates of the point A':

The general rule to reflect the coordinate across the x - axis is given by

`(x,y)\rightarrow (x,-y)`

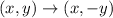
Substituting the point A(-2,3), we get;

`(-2,3)\rightarrow (-2,-3)`

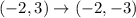
Thus, the coordinates of the point A' is (-2,-3)

Coordinates of the point B':

The general rule to reflect the coordinate across the x - axis is given by

`(x,y)\rightarrow (x,-y)`

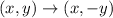
Substituting the point B(0,3), we get;

`(0,3)\rightarrow (0,-3)`

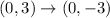
Thus, the coordinates of the point B' is (0,-3)

Coordinates of the point C':

The general rule to reflect the coordinate across the x - axis is given by

`(x,y)\rightarrow (x,-y)`

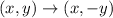
Substituting the point C(-1,-1), we get;

`(-1,-1)\rightarrow (-1,1)`

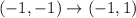
Thus, the coordinates of the point C' is (-1,1)

Hence, the coordinates of the image after a reflection over the x - axis is A'(-2,-3), B(0,-3) and C(-1,1)