Question

Which of these four sets of side lengths will form a right triangle?

Set 1
6 cm, 7 cm, StartRoot 12 EndRoot cm

Set 2
8 in., StartRoot 29 EndRoot in., StartRoot 35 EndRoot in.

Set 3
StartRoot 3 EndRoot mm, 4 mm, StartRoot 5 EndRoot mm

Set 4
9 ft, StartRoot 26 EndRoot ft, 6 ft

Set 1
Set 2
Set 3
Set 4

Answer 1

Set 2

Step-by-step explanation:

I just took the quiz on edge

Answer 2

Set 1, Set 2, Set 3

Step-by-step explanation:

In order to form a triangle:

- The longest side must be no longer than the sum of the other 2 sides

- The shortest side must be no shorter than the difference between the other 2 sides

If we call a, b, c the lengths of the 3 sides, with c = longest side and a = shortest side, this means that:

`c<a+b\\a>c-b`

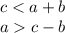
Let's now analyze the 4 sets and see if they satisfy the conditions or not:

Set 1:

a = 6 cm, b = 7 cm, c = 12 cm

We see that

12 < 6 + 7 --> OK

6 > 12 - 7 OK

So, this set can form a triangle.

Set 2:

a = 8 in, b = 29 in, c = 35 in

We see that

35 < 8 + 29 --> OK

8 > 35 - 29 --> OK

So, this set can form a triangle.

Set 3:

a = 3 mm, b = 4 mm, c = 5 mm

We see that

5 < 3+4 --> OK

3 > 5-4 --> OK

So, this set can form a triangle.

Set 4:

a = 6 ft, b = 9 ft, c = 26 ft

We see that

27 < 6 + 9 --> NO

6 > 26-9 --> NO

So, this set CANNOT form a triangle.