Answer:
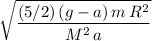 , assuming that the tension in the rope is the only tangential force on the sphere (
, assuming that the tension in the rope is the only tangential force on the sphere (
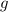 denote the gravitational acceleration.)
denote the gravitational acceleration.)
Step-by-step explanation:
The forces on the bucket are:
- Weight of the bucket:
 (downward.)
(downward.) - Tension in the rope (upward.)
Since the weight of the bucket and the tension from the rope are in opposite directions, the magnitude of the net force would be:
 .
.
The upward tension in the rope prevents the bucket from accelerating at
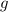 (free fall.) Rather, the bucket is accelerating at an acceleration of only
(free fall.) Rather, the bucket is accelerating at an acceleration of only
 . The net force on the bucket would be thus
. The net force on the bucket would be thus
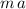 .
.
Rearrange the equation for the net force on the bucket to find the magnitude of the tension in the rope would be:
 .
.
At a distance of
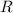 from the center of the sphere, the tension in the rope
from the center of the sphere, the tension in the rope
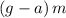 would exert a torque of
would exert a torque of
 on the sphere. If this tension is the only tangential force on this sphere, the net torque on the sphere would be
on the sphere. If this tension is the only tangential force on this sphere, the net torque on the sphere would be
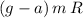 .
.
Let
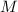 denote the mass of this sphere. The moment of inertia of this filled sphere would be
denote the mass of this sphere. The moment of inertia of this filled sphere would be
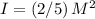 .
.
Therefore, the magnitude of the angular acceleration of this sphere would be:
 .
.
The bucket is accelerating at a magnutide of
 downwards. The rope around the sphere need to unroll at an acceleration of the same magnitude,
downwards. The rope around the sphere need to unroll at an acceleration of the same magnitude,
 . The tangential acceleration of the sphere at the surface would also need to be
. The tangential acceleration of the sphere at the surface would also need to be
 .
.
Since the surface of the sphere is at a distance of
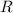 from the center, the angular acceleration of this sphere would be
from the center, the angular acceleration of this sphere would be
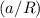 .
.
Hence the equation:
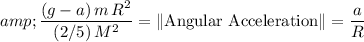 .
.
Solve this equation for
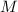 , the mass of this sphere:
, the mass of this sphere:
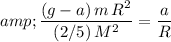 .
.
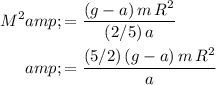 .
.
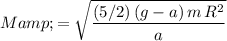 .
.