Question

What is the seventh term of the geometric sequence with a first term of 729 and a common ratio of ?

Answer 1

Given:

Given that the first term of the geometric sequence is 729.

The common ratio is
`(1)/(3)`

We need to determine the seventh term of the sequence.

Seventh term:

The seventh term of the sequence can be determined using the formula,

`a_n=a_1(r)^(n-1)`

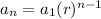
To find the seventh term, let us substitute n = 7 in the above formula, we get;

`a_7=a_1(r)^(6)`

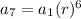
Now, substituting
`a_1= 729` and
`r=(1)/(3)`, we get;

`a_7=729((1)/(3))^(6)`

`a_7=729((1)/(729))`

`a_7=1`

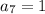
Thus, the seventh term of the geometric sequence is 1.