Question

H(x)= 9/x( x^2-49)
Determine the domain of the function

Answer 1

Answer: The domain of the function
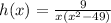`h(x) = (9)/(x(x^2-49))` is:

Interval Notation: (-∞ , -7) ∪ (-7 , 0) ∪ (0 , 7) ∪ (7, ∞)

Set-Builder Notation: x ≠ 0 , 7 , -7

All real numbers besides 0, 7, and -7.

Explanation:

In order to find the domain of your rational function, we need to simplify it:

`h(x) = (9)/(x(x^2-49)) = (9)/((x)(x+7)(x-7))`

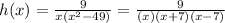
Remember, most of the time, the domain of a rational function consists of all real numbers besides zero.

To find the domain, we equal the equations in the denominator to zero.

`x=0`

`x+7=0` -->
`x=-7`

`x-7=0` -->
`x=7`

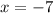
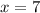
So all real numbers except for 0, -7, and 7 are in the domain of this rational function.