Question

A laser beam has diameter 1.30 mm . The beam exerts a force of 3.6×10−9 N on a totally reflecting surface.What is the amplitude of the electric field of the electromagnetic radiation in this beam?

Answer 1

`1.75\cdot 10^4 V/m`

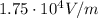
Step-by-step explanation:

For a totally reflecting surface, the radiation pressure is related to the intensity of radiation by

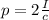`p=2(I)/(c)` (1)

where

I is the intensity of radiation

c is the speed of light

The radiation pressure is given by

`p=(F)/(A)`

where in this case:

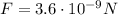`F=3.6\cdot 10^(-9)N` is the force exerted by the beam

A is the area on which the force is exerted

The beam has a diameter of d = 1.30 mm, so its area is

`A=\pi ((d)/(2))^2=\pi ((0.0013 m)/(2))^2=1.33\cdot 10^(-6) m^2`

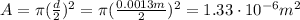
Now we can write eq(1) as

`(F)/(A)=(2I)/(c)`

From which we find the intensity of radiation, I:

`I=(Fc)/(2A)=((3.6\cdot 10^(-9))(3.0\cdot 10^8))/(2(1.33\cdot 10^(-6)))=4.06\cdot 10^5 W/m^2`

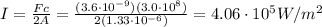
Now we can find the amplitude of the electric field using the equation

`I=(1)/(2)c\epsilon_0 E^2`

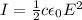
where

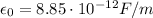`\epsilon_0=8.85\cdot 10^(-12)F/m` is the vacuum permittivity

E is the amplitude of the electric field

And solving for E,

`E=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(4.06\cdot 10^5))/((3\cdot 10^8)(8.85\cdot 10^(-12)))}=1.75\cdot 10^4 V/m`