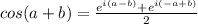Answer:
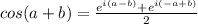
Explanation:
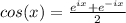
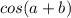
We need to expand cos(a+b) using the cos addition formula.
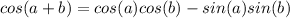
We know that we also need to use Euler's formula for sin, which is:
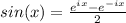 (you can get this from a similar way of getting the first result, of simply just expanding
(you can get this from a similar way of getting the first result, of simply just expanding
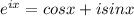 and seeing the necessary result)
and seeing the necessary result)
We can now substitute our cos's and sin's for e's
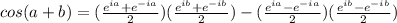
Now lets multiply out both of our terms, I'm using the exponent multiplication identity here (
 )
)
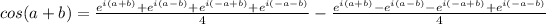
Now we can subtract these two terms.

This is starting to look a lot tidier, let's cancel the 2