Question

Geometry!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

Given:

Given that O is the center of the circle.

The radius of the circle is 3 m.

The measure of ∠AOB is 30°

We need to determine the length of the major arc ACB

Measure of major ∠AOB:

The measure of major angle AOB can be determined by subtracting 360° and 30°

Thus, we have;

`Major \ \angle AOB=360-30`

`Major \ \angle AOB=330^(\circ)`

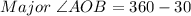
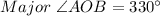
Thus, the measure of major angle is 330°

Length of the major arc ACB:

The length of the major arc ACB can be determined using the formula,

`m \widehat{ACB}=((\theta)/(360))2 \pi r`

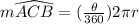
Substituting r = 3 and
`\theta=330`, we get;

`m \widehat{ACB}=((330)/(360))2 \pi (3)`

`m \widehat{ACB}=(1980)/(360)\pi`

`m \widehat{ACB}=5.5 \pi`

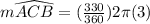
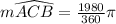
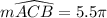
Thus, the length of the major arc ACB is 5.5π m