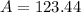Answer:
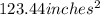
Explanation:
Total area = 2 x semi-circle + quarter-circle
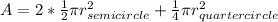
The area of a circle is
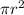 , so the area of half a circle is half this, and the area of quarter of a circle is a quarter of this.
, so the area of half a circle is half this, and the area of quarter of a circle is a quarter of this.
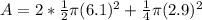
Substitute our values of pi for 3.14
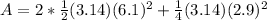
Simplify
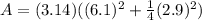
Now solve for A