Answer:
A) (20,-3)
Explanation:
we know that
If a ordered pair lie on the circle, then the ordered pair must satisfy the equation of the circle
we have
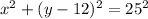
The center of the circle is the point (0,12) and the radius is r=25 units
Verify
A) (20,-3)
substitute the value of x and y in the equation and then analyze the result
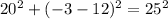
 ----> is true
----> is true
therefore
The ordered pair lie on the circle
B) (-7,24)
substitute the value of x and y in the equation and then analyze the result

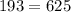 ----> is not true
----> is not true
therefore
The ordered pair not lie on the circle
C) (0,13)
substitute the value of x and y in the equation and then analyze the result
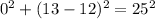
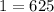 ----> is not true
----> is not true
therefore
The ordered pair not lie on the circle
D) (-25,-13)
substitute the value of x and y in the equation and then analyze the result
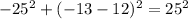
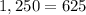 ----> is not true
----> is not true
therefore
The ordered pair not lie on the circle