Question

Circle P has secants SU and TQ as shown. What is the measure of angle R?

A) type the equation needed to solve for angle R.

B) m
a) 30 degrees
b) 73 degrees
c) 60 degrees
d) 146 degrees

Help please!

Answer 1

Given:

Given that Circle P has secants SU and TQ.

The measure of arc UT is 43° and the measure of arc SQ is 103°

We need to determine the equation to solve ∠R and the measure of ∠R.

Equation to solve for ∠R:

Since, we know the property that "if a tangent and a secant, two tangents or two secants intersect in the interior of the circle, then the measure of the angle formed is one half the difference of the measures of the intercepted arcs".

Thus, applying the above property, we have;

`\angle R=(1)/(2)(m \widehat{SQ}-m \widehat{UT})`

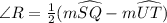
Thus, the equation to solve for ∠R is
`\angle R=(1)/(2)(m \widehat{SQ}-m \widehat{UT})`

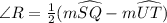
Measure of ∠R:

The measure of ∠R can be determined by substituting the values of the measure of arcs SQ and UT in the equation
`\angle R=(1)/(2)(m \widehat{SQ}-m \widehat{UT})`

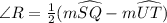
Thus, we have;

`\angle R=(1)/(2)(103^(\circ)-43^(\circ))`

`\angle R=(1)/(2)(60^(\circ))`

`\angle R=30^(\circ)`

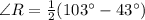
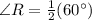
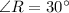
Thus, the measure of ∠R is 30°

Hence, Option a is the correct answer.