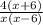Question

Help please with this question

Answer 1

Given:

The given two functions are
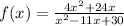`f(x)=(4 x^(2)+24 x)/(x^(2)-11 x+30)` and
`g(x)=(x-5)/(x^(2))`

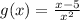
We need to determine the value of R(x)

Value of R(x):

The value of R(x) can be determined by R(x) = f(x) × g(x)

Substituting the values, we get;

`R(x)=(4 x^(2)+24 x)/(x^(2)-11 x+30) \cdot (x-5)/(x^(2))`

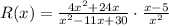
Multiplying the fractions, we have;

`R(x)=(\left(4 x^(2)+24 x\right)(x-5))/(\left(x^(2)-11 x+30\right) x^(2))`

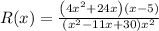
Let us factor out the common term 4x from the term (4x² + 24x)

Thus, we have;

`R(x)=(4 x(x+6)(x-5))/(\left(x^(2)-11 x+30\right) x^(2))`

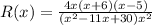
Let us factor the term (x² -11x + 30), we get;

`R(x)=(4(x+6)(x-5))/(x(x-5)(x-6))`

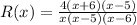
Cancelling the common term, we have;

`R(x)=(4(x+6))/(x(x-6))`

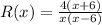
Thus, the value of R(x) is
`(4(x+6))/(x(x-6))`